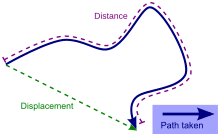
Displacement

Displacement (geometry)

Displacement versus distance traveled along a path

In geometry, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position.

A displacement may be also described as a relative position resulting from the motion, that is, as the final position x_f of a point relatively to its initial position x_i. The corresponding displacement vector can be defined as the difference between the final and initial positions:

${\displaystyle {s}={x_{\textrm {f}}-x_{\textrm {i}}}=\Delta {x}}$

In considering motions of objects over time, the instantaneous velocity of the object is the rate of change of the displacement as a function of time. The instantaneous speed, then, is distinct from velocity, or the time rate of change of the distance traveled along a specific path. The velocity may be equivalently defined as the time rate of change of the position vector. If one considers a moving initial position, or equivalently a moving origin (e.g. an initial position or origin which is fixed to a train wagon, which in turn moves with respect to its rail track), the velocity of P (e.g. a point representing the position of a passenger walking on the train) may be referred to as a relative velocity, as opposed to an absolute velocity, which is computed with respect to a point which is considered to be 'fixed in space' (such as, for instance, a point fixed on the floor of the train station).

For motion over a given interval of time, the displacement divided by the length of the time interval defines the average velocity. (Note that the average velocity, as a vector, differs from the average speed that is the ratio of the path length — a scalar — and the time interval.)

DerivativesEdit

For a position vector ${\displaystyle \mathbf {s} }$ that is a function of time ${\displaystyle t}$, the derivatives can be computed with respect to ${\displaystyle t}$. The first two derivatives are frequently encountered in physics.

Velocity

${\displaystyle {\textbf {v}}={\frac {d{\textbf {s}}}{dt}}}$

Acceleration

${\displaystyle {\textbf {a}}={\frac {d{\textbf {v}}}{dt}}={\frac {d^{2}{\boldsymbol {s}}}{dt^{2}}}}$

Jerk

${\displaystyle {\textbf {j}}={\frac {d{\textbf {a}}}{dt}}={\frac {d^{2}{\textbf {v}}}{dt^{2}}}={\frac {d^{3}{\textbf {s}}}{dt^{3}}}}$

These common names correspond to terminology used in basic kinematics. By extension, the higher order derivatives can be computed in a similar fashion. Study of these higher order derivatives can improve approximations of the original displacement function. Such higher-order terms are required in order to accurately represent the displacement function as a sum of an infinite series, enabling several analytical techniques in engineering and physics. The fourth order derivative is called jounce.-