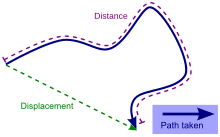
Displacement

Displacement (geometry)

Displacement versus distance traveled along a path

In geometry, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position.

A displacement may be also described as a relative position resulting from the motion, that is, as the final position x_f of a point relatively to its initial position x_i. The corresponding displacement vector can be defined as the difference between the final and initial positions:

${\displaystyle {s}={x_{\textrm {f}}-x_{\textrm {i}}}=\Delta {x}}$

In considering motions of objects over time, the instantaneous velocity of the object is the rate of change of the displacement as a function of time. The instantaneous speed, then, is distinct from velocity, or the time rate of change of the distance traveled along a specific path. The velocity may be equivalently defined as the time rate of change of the position vector. If one considers a moving initial position, or equivalently a moving origin (e.g. an initial position or origin which is fixed to a train wagon, which in turn moves with respect to its rail track), the velocity of P (e.g. a point representing the position of a passenger walking on the train) may be referred to as a relative velocity, as opposed to an absolute velocity, which is computed with respect to a point which is considered to be 'fixed in space' (such as, for instance, a point fixed on the floor of the train station).

For motion over a given interval of time, the displacement divided by the length of the time interval defines the average velocity. (Note that the average velocity, as a vector, differs from the average speed that is the ratio of the path length — a scalar — and the time interval.)

DerivativesEdit

For a position vector ${\displaystyle \mathbf {s} }$ that is a function of time ${\displaystyle t}$, the derivatives can be computed with respect to ${\displaystyle t}$. The first two derivatives are frequently encountered in physics.

Velocity

${\displaystyle {\textbf {v}}={\frac {d{\textbf {s}}}{dt}}}$

Acceleration

${\displaystyle {\textbf {a}}={\frac {d{\textbf {v}}}{dt}}={\frac {d^{2}{\boldsymbol {s}}}{dt^{2}}}}$

Jerk

${\displaystyle {\textbf {j}}={\frac {d{\textbf {a}}}{dt}}={\frac {d^{2}{\textbf {v}}}{dt^{2}}}={\frac {d^{3}{\textbf {s}}}{dt^{3}}}}$

These common names correspond to terminology used in basic kinematics. By extension, the higher order derivatives can be computed in a similar fashion. Study of these higher order derivatives can improve approximations of the original displacement function. Such higher-order terms are required in order to accurately represent the displacement function as a sum of an infinite series, enabling several analytical techniques in engineering and physics. The fourth order derivative is called jounce.- 

Kinematic formulas

Search for courses,

Main contentKinematic formulas and projectile motion

What are the kinematic formulas?

Here are the main equations you can use to analyze situations with constant acceleration.

What are the kinematic formulas?

The kinematic formulas are a set of formulas that relate the five kinematic variables listed below.

$\Delta x\quad\text{Displacement}$delta, x, start text, D, i, s, p, l, a, c, e, m, e, n, t, end text
$t\qquad\text{Time interval}~$t, start text, T, i, m, e, space, i, n, t, e, r, v, a, l, end text, space
$v_0 ~~\quad\text{Initial velocity}~$v, start subscript, 0, end subscript, space, space, start text, I, n, i, t, i, a, l, space, v, e, l, o, c, i, t, y, end text, space
$v\quad ~~~\text{Final velocity}~$v, space, space, space, start text, F, i, n, a, l, space, v, e, l, o, c, i, t, y, end text, space
$a \quad~~ \text{ Constant acceleration}~$a, space, space, start text, space, C, o, n, s, t, a, n, t, space, a, c, c, e, l, e, r, a, t, i, o, n, end text, space

Why is the time interval now written as t?

$t$t$\Delta x$delta, x$\Delta t$delta, t$\Delta$delta$t$t

$t$t$\Delta t$delta, t

If we know three of these five kinematic variables—$\Delta x, t, v_0, v, a$delta, x, comma, t, comma, v, start subscript, 0, end subscript, comma, v, comma, a—for an object under constant acceleration, we can use a kinematic formula, see below, to solve for one of the unknown variables.

The kinematic formulas are often written as the following four equations.

Where did these formulas come from?

$\Large 1. \quad v=v_0+at$1, point, v, equals, v, start subscript, 0, end subscript, plus, a, t

$\Large 2. \quad {\Delta x}=(\dfrac{v+v_0}{2})t$2, point, delta, x, equals, left parenthesis, start fraction, v, plus, v, start subscript, 0, end subscript, divided by, 2, end fraction, right parenthesis, t

$\Large 3. \quad \Delta x=v_0 t+\dfrac{1}{2}at^2$3, point, delta, x, equals, v, start subscript, 0, end subscript, t, plus, start fraction, 1, divided by, 2, end fraction, a, t, squared

$\Large 4. \quad v^2=v_0^2+2a\Delta x$4, point, v, squared, equals, v, start subscript, 0, end subscript, squared, plus, 2, a, delta, x

Since the kinematic formulas are only accurate if the acceleration is constant during the time interval considered, we have to be careful to not use them when the acceleration is changing. Also, the kinematic formulas assume all variables are referring to the same direction: horizontal $x$x, vertical $y$y, etc.

Wait, what?

$v_{0x}$v, start subscript, 0, x, end subscript$\Delta x, v_x, a_x$delta, x, comma, v, start subscript, x, end subscript, comma, a, start subscript, x, end subscript

$v_{0y}$v, start subscript, 0, y, end subscript$\Delta y, v_y, a_y$delta, y, comma, v, start subscript, y, end subscript, comma, a, start subscript, y, end subscript

$x$x

$v_x=v_{0x}+a_xt$v, start subscript, x, end subscript, equals, v, start subscript, 0, x, end subscript, plus, a, start subscript, x, end subscript, t

$\Delta x=v_{0x} t+\dfrac{1}{2}a_xt^2$delta, x, equals, v, start subscript, 0, x, end subscript, t, plus, start fraction, 1, divided by, 2, end fraction, a, start subscript, x, end subscript, t, squared

$v_x^2=v_{0x}^2+2a_x\Delta x$v, start subscript, x, end subscript, squared, equals, v, start subscript, 0, x, end subscript, squared, plus, 2, a, start subscript, x, end subscript, delta, x

$\dfrac{v_x+v_{0x}}{2}=\dfrac{\Delta x}{t}$start fraction, v, start subscript, x, end subscript, plus, v, start subscript, 0, x, end subscript, divided by, 2, end fraction, equals, start fraction, delta, x, divided by, t, end fraction

What is a freely flying object—i.e., a projectile?

It might seem like the fact that the kinematic formulas only work for time intervals of constant acceleration would severely limit the applicability of these formulas. However one of the most common forms of motion, free fall, just happens to be constant acceleration.

All freely flying objects—also called projectiles—on Earth, regardless of their mass, have a constant downward acceleration due to gravity of magnitude $g=9.81\dfrac{\text{m}}{\text{s}^2}$g, equals, 9, point, 81, start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction.

$\Large g=9.81\dfrac{\text{m}}{\text{s}^2}\quad \text{(Magnitude of acceleration due to gravity)}$g, equals, 9, point, 81, start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction, start text, left parenthesis, M, a, g, n, i, t, u, d, e, space, o, f, space, a, c, c, e, l, e, r, a, t, i, o, n, space, d, u, e, space, t, o, space, g, r, a, v, i, t, y, right parenthesis, end text

A freely flying object is defined as any object that is accelerating only due to the influence of gravity. We typically assume the effect of air resistance is small enough to ignore, which means any object that is dropped, thrown, or otherwise flying freely through the air is typically assumed to be a freely flying projectile with a constant downward acceleration of magnitude $g=9.81\dfrac{\text{m}}{\text{s}^2}$g, equals, 9, point, 81, start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction.

This is both strange and lucky if we think about it. It's strange since this means that a large boulder will accelerate downwards with the same acceleration as a small pebble, and if dropped from the same height, they would strike the ground at the same time.

How can this be so?

It's lucky since we don't need to know the mass of the projectile when solving kinematic formulas since the freely flying object will have the same magnitude of acceleration, $g=9.81\dfrac{\text{m}}{\text{s}^2}$g, equals, 9, point, 81, start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction, no matter what mass it has—as long as air resistance is negligible.

Note that $g=9.81\dfrac{\text{m}}{\text{s}^2}$g, equals, 9, point, 81, start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction is just the magnitude of the acceleration due to gravity. If upward is selected as positive, we must make the acceleration due to gravity negative $a_y=-9.81\dfrac{\text{m}}{\text{s}^2}$a, start subscript, y, end subscript, equals, minus, 9, point, 81, start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction for a projectile when we plug into the kinematic formulas.

Warning: Forgetting to include a negative sign is one of the most common sources of error when using kinematic formulas.